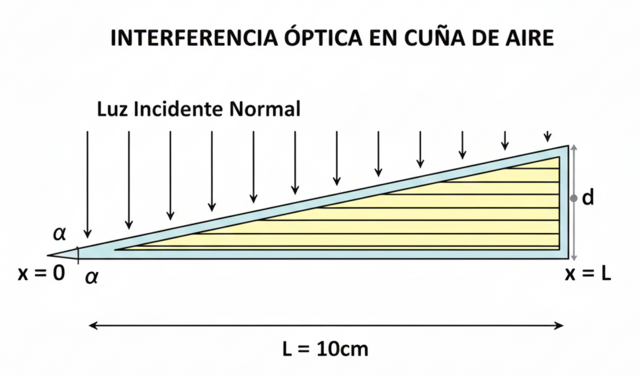
Se dispone de dos láminas planas de vidrio, cuyo índice de refracción es $$$ \text{n}_\text{v} = 1.5$$$, de longitud L = 10 cm. Una de ellas se apoya sobre la otra, pero en un extremo se separa mediante un alambre delgado de diámetro «d», formando una cuña de aire de ángulo muy pequeño «$$$ \alpha$$$», como se muestra en la figura:

El índice de refracción del aire es $$$ \text{n}_\text{a} = 1.0$$$. Se ilumina el sistema desde arriba con luz incidente normal a las láminas.

Parte A:

Cuando se utiliza luz monocromática de longitud de onda $$$ \lambda = 600\ \text{nm}$$$, se observa un patrón de interferencia formado por franjas brillantes y oscuras. A lo largo de toda la longitud «L» se cuentan exactamente 20 franjas brillantes. Calcula:

i) El ángulo «$$$ \alpha$$$» de la cuña de aire.

ii) El diámetro «d» del alambre.

Parte B:

Ahora se ilumina la cuña con luz blanca, el espectro visible recorre los valores de longitud de onda desde 400 nm a 700 nm. Describe cualitativamente qué se observa en:

iii) El extremo donde las láminas están en contacto, «x = 0».

iv) En una posición ubicada a «x = 2 cm» del borde de contacto.