Ejercicios FyQ
Se tienen 4 g de una disolución de ácido nítrico () al en peso. ¿Cuál es su concentración en g/L si la densidad de la disolución es de 1.17 g/mL?
Clica aquí para acceder al enunciado y las respuestas del problema que se resuelve en el vídeo.
Ejercicios Resueltos, Situaciones de aprendizaje y VÍDEOS de Física y Química para Secundaria y Bachillerato
Últimos artículos
[P(8001)] EBAU Madrid: física (junio 2022) - ejercicio A.3 (8007) EBAU Madrid: física (junio 2022) - ejercicio A.3 (8001) La figura representa una varilla metálica de 20 cm de longitud, cuyos extremos deslizan sin rozamiento sobre unos raíles horizontales, paralelos al eje x, metálicos y de resistencia despreciable. La varilla tiene resistencia despreciable y su velocidad es
. Los raíles están conectados en x = 0 por una resistencia de valor 
. En la región hay un campo magnético uniforme 
.
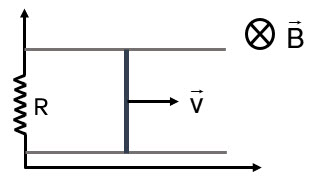
Calcula:
a) La intensidad de la corriente en el circuito formado por la varilla, la resistencia y los tramos de raíl entre ellas.
b) La fuerza
que el campo magnético ejerce sobre la varilla.[P(7999)] EBAU Madrid: física (junio 2022) - ejercicio A.1 (8003) Puedes ver el enunciado y las respuestas del problema resuelto en el vídeo si haces clic aquí.
EBAU Madrid: física (junio 2022) - ejercicio A.2 (8000) Por una cuerda dispuesta a lo largo del eje x viaja una onda armónica que desplaza los elementos de la cuerda en la dirección del eje y. Se sabe que los elementos A y B, respectivamente ubicados en
y 
, oscilan en fase y cortan al eje x cada 4 s. Teniendo en cuenta que no hay entre A y B ningún otro elemento que oscile en fase con ellos:a) Calcula el valor de la velocidad de propagación.
b) Escribe a la expresión matemática de la onda, si esta viaja en el sentido negativo del eje x y en el instante inicial los elementos A y B presentan desplazamiento igual a +10 cm y velocidad nula.
EBAU Madrid: física (junio 2022) - ejercicio A.1 (7999) Una partícula de masa 20 kg permanece fija en el origen de coordenadas.
a) Calcula el campo gravitatorio generado por la masa en el punto (8, 6) m y la fuerza que experimentará una segunda partícula de masa 3 kg situada en dicho punto.
b) Con el objetivo de alejar la segunda partícula, se le transmite una velocidad de
en la dirección de la recta que une ambas partículas. Halla el punto más alejado del origen que alcanzará dicha partícula.Dato:
